STEP4:全体系弾性方程式の組み立て
対象構造物の節点変位は、第一に、その構造物を適当に分割して要素の集合体とみなしてその各要素(ローカル)について弾性方程式を離散化を行い、第二に、その構造物全体について全体系(グローバル)の弾性方程式を組み立てて、最後に、この線型方程式を解くという過程を経て求められます。 以下では、第二、第三のステップについて話を展開していきます。
全体系弾性方程式を組み立てる条件
全体系弾性方程式を組み立てるには、①変位の適合条件、②力のつり合い条件、がいたるところで成立していなければなりません。このとき①については、各要素につけたローカルな節点番号に対し、グローバルな節点番号を対象構造物の全要素にふり、全体についての変位系\(\vec{u}\)を \begin{equation} \vec{u}=\begin{bmatrix} \vec{u_1} \\ \vec{u_2} \\ \vdots \\ \vec{u_n} \end{bmatrix} \end{equation} と規定すれば、適切な形状関数を選択することにより、自動的に満足されます。 次に②の条件については、構造物に外力\(\,\vec{T}\,\)が各節点に作用すると考えると\(\,\vec{T}\,\)は、 \begin{equation} \vec{T}=\begin{bmatrix} \vec{T_1} \\ \vec{T_2} \\ \vdots \\ \vec{T_n} \end{bmatrix} \\ \end{equation} で表されます。ここで任意の節点に着目し、それを有する要素の弾性方程式をグローバルな節点番号でマトリクス表示すると、例えば、 \begin{equation} \begin{bmatrix} K^{e}_{aa} & K^{e}_{ab} & \ldots & K^{e}_{ai} & \ldots & K^{e}_{an} \\ K^{e}_{ba} & K^{e}_{bb} & \ldots & K^{e}_{bi} & \ldots & K^{e}_{bn} \\ \vdots & \vdots & \ddots & \vdots & & \vdots\\ K^{e}_{ia} & K^{e}_{ib} & \ldots & K^{e}_{ii} & \ldots & K^{e}_{in} \\ \vdots & \vdots & & \vdots & \ddots & \vdots\\ K^{e}_{na} & K^{e}_{nb} & \ldots & K^{e}_{ni} & \ldots & K^{e}_{nn} \\ \end{bmatrix} \cdot \begin{bmatrix} \vec{u^{e}_{a}}\\ \vec{u^{e}_{b}}\\ \vdots\\ \vec{u^{e}_{i}}\\ \vdots\\ \vec{u^{e}_{n}}\\ \end{bmatrix} = \begin{bmatrix} \vec{T^{e}_{a}}\\ \vec{T^{e}_{b}}\\ \vdots\\ \vec{T^{e}_{i}}\\ \vdots\\ \vec{T^{e}_{n}}\\ \end{bmatrix} + \begin{bmatrix} \vec{F^{e}_{a}}\\ \vec{F^{e}_{b}}\\ \vdots\\ \vec{F^{e}_{i}}\\ \vdots\\ \vec{F^{e}_{n}}\\ \end{bmatrix} \end{equation} となりますから、その要素に係る\(\,i\,\)行の外力は、 \begin{equation} \vec{T^e_i}=K^e_{ia}\vec{u^e_a}+K^e_{ib}\vec{u^e_b}+\cdots+K^e_{in}\vec{u^e_n}-\vec{F^e_i} \end{equation} となります。節点\(\,i\,\)における外力\(\,\vec{T_i}\,\)は、節点\(\,i\,\)を有する全ての要素からの力の総和と等価にならなくてはなりませんので、 \begin{eqnarray} \vec{T_i}=\left(\sum^m_{e=1}K^e_{i1} \right)\vec{u_1}+\left(\sum^m_{e=1}K^e_{i2} \right)\vec{u_2}+\cdots+\left(\sum^m_{e=1}K^e_{in} \right)\vec{u_n}-\vec{F_i} \\ \vec{F_i}=\sum^m_{e=1}\vec{F^e_i} \notag \end{eqnarray} となります。したがって全体剛性マトリクスを含む全体系弾性方程式は、変位の適合条件も考慮することにより、次のように組み立てればよいことになります。 \begin{equation} \begin{bmatrix} \left(\displaystyle \sum^m_{e=1}K^{e}_{11} \right)\\ \vdots\\ \left(\displaystyle \sum^m_{e=1}K^{e}_{i1} \right) & \cdots & \left(\displaystyle \sum^m_{e=1}K^{e}_{ii} \right) & \cdots & \left(\displaystyle \sum^m_{e=1}K^{e}_{in} \right)\\ & & & & \vdots\\ & & & & \left(\displaystyle \sum^m_{e=1}K^{e}_{nn} \right) \\ \end{bmatrix} \cdot \begin{bmatrix} \vec{u_1}\\ \vdots\\ \vec{u_i}\\ \vdots\\ \vec{u_n}\\ \end{bmatrix} = \begin{bmatrix} \vec{T_1}\\ \vdots\\ \vec{T_i}\\ \vdots\\ \vec{T_n}\\ \end{bmatrix} + \begin{bmatrix} \vec{F_1}\\ \vdots\\ \vec{F_i}\\ \vdots\\ \vec{F_n}\\ \end{bmatrix} \label{76} \end{equation}
全体剛性マトリクスの組み立て
前述した全体剛性マトリクスを具体的に組み立てるために、4つの要素からなる構造物を仮定します。 そして、各要素に1~4の要素番号をふり、それがこの順に4、3、2、2の節点数を有すると仮定します。このとき全体系の節点数は6であるとして表1.2のように全体系の節点番号(住所)に対応しているとすると、
| 要素番号 | 節点番号 |
|---|---|
| 1 | 1, 2, 5, 6 |
| 2 | 2, 4, 6 |
| 3 | 2, 3 |
| 4 | 3, 4 |
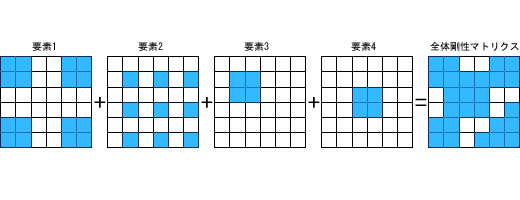
図2 要素剛性マトリクスから組み立てられた全体剛性マトリクス
\begin{equation} K^e_{mn}=\sum^3_{k=1} \sum^3_{j=1} \sum^3_{i=1} \left\{ \sum^6_{p=1} \left( B_{mp}^{\mathrm{T}} \cdot \sum^6_{q=1} D_{pq} B_{qn} \right) \right\}_{ijk}|\boldsymbol{J}|w_i w_j w_k \label{64} \end{equation} で与えられた要素剛性マトリクスの各成分は、先述の条件にしたがって式\eqref{76}のように適当な住所に加え込まれていきます。この状況を図示したものが図2です。この図中の青色のハッチが剛性マトリクスの部分マトリクス\(\,K_{ij}\,\)を表しています。このように、全体系剛性マトリクスは、それを組み立てる際の幾何的特性から必ず対称形になるのが特徴です。
境界条件による全体系弾性方程式の規模最小化
境界条件は、通常、変位あるいは表面荷重で与えられます。ここで全体系弾性方程式を組み立てる際、そのまま組み立てると全体剛性マトリクスは図2の形 \begin{equation} \begin{bmatrix} K_{11} & K_{12} & & & K_{15} & K_{16} \\ K_{21} & K_{22} & K_{23} & K_{24} & K_{25} & K_{26} \\ & K_{32} & K_{33} & K_{34}& & \\ & K_{42} & K_{43} & K_{44} & & K_{46} \\ K_{51} & K_{52} & & & K_{55} & K_{56} \\ K_{61} & K_{62} & & K_{64} & K_{65} & K_{66} \end{bmatrix} \cdot \\ \begin{bmatrix} \vec{u_1}\\ \vec{u_2}\\ \vec{u_3}\\ \vec{u_4}\\ \vec{u_5}\\ \vec{u_6}\\ \end{bmatrix}= \begin{bmatrix} \vec{F_1}\\ \vec{F_2}\\ \vec{F_3}\\ \vec{F_4}\\ \vec{F_5}\\ \vec{F_6}\\ \end{bmatrix} \label{77} \end{equation} になります。このとき仮に、変位\(\,\vec{u_2}\,\)、\(\,\vec{u_6}\,\)が固定されていて、\(\,\vec{u^*_2}\,\)、\(\,\vec{u^*_6}\,\)として既知であるとするば、即それらに寄与する剛性マトリクスの成分を次のように荷重ベクトルから控除することができ、結果的に全体の方程式数を減らすことができます。 \begin{equation} \begin{bmatrix} K_{11} & & & K_{15} \\ & K_{33} & K_{34} & \\ & K_{43} & K_{44} & \\ K_{51} & & & K_{55} \\ \end{bmatrix} \cdot \\ \begin{bmatrix} \vec{u_1}\\ \vec{u_3}\\ \vec{u_4}\\ \vec{u_5}\\ \end{bmatrix}= \begin{bmatrix} \vec{F_1}-K_{12}\vec{u^*_2}-K_{16}\vec{u^*_6}\\ \vec{F_3}-K_{32}\vec{u^*_2}\\ \vec{F_4}-K_{42}\vec{u^*_2}-K_{46}\vec{u^*_6}\\ \vec{F_5}-K_{52}\vec{u^*_2}-K_{56}\vec{u^*_6} \end{bmatrix} \end{equation}