STEP２：弾性方程式の離散化（前編）

仮想仕事の原理

弾性方程式を離散化するにあたって、釣合いの状態にある構造物に仮想仕事の原理を適用します。構造物に仮想変位を与えると、その変分が微小のときにはつり合いの状態にあると考えられ、外力と内力のなす仕事の総和は0(大きさが等価）となります。すなわち外力のなす仮想仕事を\(\,\delta W\,\)、内力のなす仮想仕事を\(\,\delta U\,\)とすると、\begin{equation} \delta W + \delta U = 0 \label{10} \end{equation} が成立します。これは以下によって証明されます。

内力のなす仮想仕事として仮想変位\(\,\delta u_i\,\)に対する歪みエネルギー\(\,\delta U\,\)は体積力による仕事量を基準にとると、\begin{equation} \delta U = \int\sigma_{ij} \delta \varepsilon_{ij} \, d\Omega - \int F_i \delta u_i \, d\Omega \label{11} \end{equation} で与えられます。 ここで、\(\sigma_{ij}\)、\(\delta u_j\,\)は微分可能（「微分・中微分」\(\partial\sigma_{ij}=\sigma^{\prime}_{ij}\partial x_j\)、\(\partial(\delta u_i)=\delta u_i^{\prime}\partial x_j\)）ですから、 \begin{eqnarray} \{\sigma_{ij}\delta u_i\}^{\prime} &=& \sigma_{ij}^{\prime}\delta u_i + \sigma_{ij}\delta u_i^{\prime} \notag \\ \sigma_{ij}\delta u_i^{\prime} &=& \{\sigma_{ij}\delta u_i\}^{\prime} - \sigma_{ij}^{\prime}\delta u_i \notag \\ \therefore \sigma_{ij}\dd{(\delta u_i)}{x_j} &=& \dd{(\sigma_{ij}\delta u_i)}{x_j} -\dd{\sigma_{ij}}{x_j}\delta u_i \notag \end{eqnarray} という関係式（部分積分）が成り立ちます。この両辺を体積\(\,\Omega\,\)で積分すると \begin{equation} \int\sigma_{ij} \dd{(\delta u_i)}{x_j} \, d\Omega = \int \dd{(\sigma_{ij} \delta u_i)}{x_j} \, d\Omega - \int \delta u_i\dd{\sigma_{ij}}{x_j} \, d\Omega \notag \end{equation} となります。左辺に歪の定義式 \begin{equation} \delta \varepsilon_{ij} = \dd{(\delta u_i)}{x_j} \end{equation} を用いて整理すると \begin{equation} \int\sigma_{ij} \delta \varepsilon_{ij} \, d\Omega = \int \dd{(\sigma_{ij} \delta u_i)}{x_j} \, d\Omega - \int \delta u_i\dd{\sigma_{ij}}{x_j} \, d\Omega \end{equation} となりますので、式\eqref{11}は、 \begin{equation} \delta U = \int \dd{(\sigma_{ij} \delta u_i)}{x_j} \, d\Omega - \int \delta u_i\dd{\sigma_{ij}}{x_j}\, d\Omega - \int F_i \delta u_i \, d\Omega \label{14} \end{equation} となり、また、ここでガウスのDivergence theory： \begin{equation} \int f_{j,j} \, d\Omega = \int f_j n_j d\Gamma \end{equation} を式\eqref{14}に用いると、 \begin{align} \delta U &= \int \sigma_{ij} \delta u_{i} n_{j} \, d\Gamma - \int \delta u_{i} \dd{\sigma_{ij}}{x_{j}} \, d\Omega - \int F_{i} \delta u_{i} \, d\Omega \notag\\ &= - \int T_{j} \delta u_{j} \, d\Gamma - \int \delta u_{i} \left( \dd{\sigma_{ij}}{x_{j}} + F_{i} \right) \, d\Omega \label{16} \end{align} となります。一方,外力のなす仮想仕事として表面応力\(\,T_j\,\)による仮想仕事\(\,\delta W \,\)は、 \begin{equation} \delta W = \int T_j \delta u_j \, d\Gamma \label{17} \end{equation} ですから、式\eqref{16}および\eqref{17}により、 \begin{equation} \delta W + \delta U = - \int \delta u_i \left( \dd{\sigma_{ij}}{x_j} + F_i \right) \, d\Omega \end{equation} となります。上式で構造物がつり合いの状態にあるときには、 \begin{equation} \dd{\sigma_{ij}}{x_j} + F_i = 0 \end{equation} が成り立っているので、以上により、 \begin{equation} \delta W + \delta U = 0 \end{equation} が得られます。■

形状関数の導入

直行座標系における現実のモノは、通常複雑な形状であるため、それを4面体要素に分割する際に任意にゆがんだ形状になることが避けられません。このようなときには、局所座標系の立方体要素で問題を処理して、その後、直行座標系に写像することが大変有効です。そこで図１の\(\,(\xi,\eta, \zeta)\,\)で表される局所座標系にて20節点を有する立方体要素\(\,(-1\leqq \xi,\eta,\zeta \leqq 1)\,\)を定義して、これらの節点における変位を規定することによって、要素内の任意点における未知量を求められるように形状関数を導入します。すなわち、形状関数\(\,N_i(\xi_i,\eta_i, \zeta_i)\,\)として、

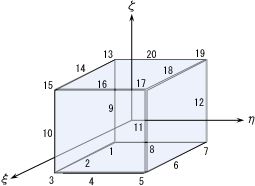
図１ 局所座標系20節点要素

20節点要素の形状関数

\begin{eqnarray} &N_1 &=& \frac{1}{8}(1-\xi)(1-\eta)(1-\zeta)(-\xi-\eta-\zeta-2) \notag \\ &\dd{N_1}{\xi}&=&\frac{1}{8}(1-\eta)(1-\zeta)(2\xi+\eta+\zeta+1) \notag \\ &\dd{N_1}{\eta}&=&\frac{1}{8}(1-\xi)(1-\zeta)(\xi+2\eta+\zeta+1) \notag \\ &\dd{N_1}{\zeta}&=&\frac{1}{8}(1-\xi)(1-\eta)(\xi+\eta+2\zeta+1) \notag \end{eqnarray} \begin{eqnarray} &N_2 &=& \frac{1}{4}(1-\xi \cdot \xi)(1-\eta)(1-\zeta) \notag \notag \\ &\dd{N_2}{\xi}&=&-\frac{1}{2}\xi(1-\eta)(1-\zeta) \notag \notag \\ &\dd{N_2}{\eta}&=&-\frac{1}{4}(1-\xi \cdot \xi)(1-\zeta) \notag \\ &\dd{N_2}{\zeta}&=&-\frac{1}{4}(1-\xi \cdot \xi)(1-\eta) \notag \end{eqnarray} \begin{eqnarray} &N_3&=&\frac{1}{8}(1+\xi)(1-\eta)(1-\zeta)(\xi-\eta-\zeta-2) \notag \\ &\dd{N_3}{\xi}&=&\frac{1}{8}(1-\eta)(1-\zeta)(2\xi-\eta-\zeta-1) \notag \\ &\dd{N_3}{\eta}&=&\frac{1}{8}(1+\xi)(1-\zeta)(-\xi+2\eta+\zeta+1) \notag \\ &\dd{N_3}{\zeta}&=&\frac{1}{8}(1+\xi)(1-\eta)(-\xi+\eta+2\zeta+1) \notag \end{eqnarray} \begin{eqnarray} &N_4&=&\frac{1}{4}(1+\xi)(1-\eta \cdot \eta)(1-\zeta) \notag \\ &\dd{N_4}{\xi}&=&\frac{1}{4}(1-\eta \cdot \eta)(1-\zeta) \notag \\ &\dd{N_4}{\eta}&=&-\frac{1}{2}\eta(1+\xi)(1-\zeta) \notag \\ &\dd{N_4}{\zeta}&=&-\frac{1}{4}(1+\xi)(1-\eta \cdot \eta) \notag \end{eqnarray} \begin{eqnarray} &N_5&=&\frac{1}{8}(1+\xi)(1+\eta)(1-\zeta)(\xi+\eta-\zeta-2) \notag \\ &\dd{N_5}{\xi}&=&\frac{1}{8}(1+\eta)(1-\zeta)(2\xi+\eta-\zeta-1) \notag \\ &\dd{N_5}{\eta}&=&\frac{1}{8}(1+\xi)(1-\zeta)(\xi+2\eta-\zeta-1) \notag \\ &\dd{N_5}{\zeta}&=&\frac{1}{8}(1+\xi)(1+\eta)(-\xi-\eta+2\zeta+1) \notag \end{eqnarray} \begin{eqnarray} &N_6&=&\frac{1}{4}(1-\xi \cdot \xi)(1+\eta)(1-\zeta) \notag \\ &\dd{N_6}{\xi}&=&-\frac{1}{2}\xi(1+\eta)(1-\zeta) \notag \\ &\dd{N_6}{\eta}&=&\frac{1}{4}(1-\xi \cdot \xi)(1-\zeta) \notag \\ &\dd{N_6}{\zeta}&=&-\frac{1}{4}(1-\xi \cdot \xi)(1+\eta) \notag \end{eqnarray} \begin{eqnarray} &N_7&=&\frac{1}{8}(1-\xi)(1+\eta)(1-\zeta)(-\xi+\eta-\zeta-2) \notag \\ &\dd{N_7}{\xi}&=&\frac{1}{8}(1+\eta)(1-\zeta)(2\xi-\eta+\zeta+1) \notag \\ &\dd{N_7}{\eta}&=&\frac{1}{8}(1-\xi)(1-\zeta)(-\xi+2\eta-\zeta-1) \notag \\ &\dd{N_7}{\zeta}&=&\frac{1}{8}(1-\xi)(1+\eta)(\xi-\eta+2\zeta+1) \notag \end{eqnarray} \begin{eqnarray} &N_8&=&\frac{1}{4}(1-\xi)(1-\eta \cdot \eta)(1-\zeta) \notag \\ &\dd{N_8}{\xi}&=&-\frac{1}{4}(1-\eta \cdot \eta)(1-\zeta) \notag \\ &\dd{N_8}{\eta}&=&-\frac{1}{2}\eta(1-\xi)(1-\zeta) \notag \\ &\dd{N_8}{\zeta}&=&-\frac{1}{4}(1-\xi)(1-\eta \cdot \eta) \notag \end{eqnarray} \begin{eqnarray} &N_9&=&\frac{1}{4}(1-\xi)(1-\eta)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_9}{\xi}&=&-\frac{1}{4}(1-\eta)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_9}{\eta}&=&-\frac{1}{4}(1-\xi)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_9}{\zeta}&=&-\frac{1}{2}\zeta(1-\xi)(1-\eta) \notag \end{eqnarray} \begin{eqnarray} &N_{10}&=&\frac{1}{4}(1+\xi)(1-\eta)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_{10}}{\xi}&=&\frac{1}{4}(1-\eta)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_{10}}{\eta}&=&-\frac{1}{4}(1+\xi)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_{10}}{\zeta}&=&-\frac{1}{2}\zeta(1+\xi)(1-\eta) \notag \end{eqnarray} \begin{eqnarray} &N_{11}&=&\frac{1}{4}(1+\xi)(1+\eta)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_{11}}{\xi}&=&\frac{1}{4}(1+\eta)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_{11}}{\eta}&=&\frac{1}{4}(1+\xi)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_{11}}{\zeta}&=&-\frac{1}{2}\zeta(1+\xi)(1+\eta) \notag \end{eqnarray} \begin{eqnarray} &N_{12}&=&\frac{1}{4}(1-\xi)(1+\eta)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_{12}}{\xi}&=&-\frac{1}{4}(1+\eta)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_{12}}{\eta}&=&\frac{1}{4}(1-\xi)(1-\zeta \cdot \zeta) \notag \\ &\dd{N_{12}}{\zeta}&=&-\frac{1}{2}\zeta(1-\xi)(1+\eta) \notag \end{eqnarray} \begin{eqnarray} &N_{13}&=&\frac{1}{8}(1-\xi)(1-\eta)(1-\zeta)(-\xi-\eta+\zeta-2) \notag \\ &\dd{N_{13}}{\xi}&=&\frac{1}{8}(1-\eta)(1+\zeta)(2\xi+\eta-\zeta+1) \notag \\ &\dd{N_{13}}{\eta}&=&\frac{1}{8}(1-\xi)(1+\zeta)(\xi+2\eta-\zeta+1) \notag \\ &\dd{N_{13}}{\zeta}&=&\frac{1}{8}(1-\xi)(1-\eta)(-\xi-\eta+2\zeta-1) \notag \end{eqnarray} \begin{eqnarray} &N_{14}&=&\frac{1}{4}(1-\xi \cdot \xi)(1-\eta)(1+\zeta) \notag \\ &\dd{N_{14}}{\xi}&=&-\frac{1}{2}\xi(1-\eta)(1+\zeta) \notag \\ &\dd{N_{14}}{\eta}&=&-\frac{1}{4}(1-\xi \cdot \xi)(1+\zeta) \notag \\ &\dd{N_{14}}{\zeta}&=&\frac{1}{4}(1-\xi \cdot \xi)(1-\eta) \notag \end{eqnarray} \begin{eqnarray} &N_{15}&=&\frac{1}{8}(1+\xi)(1-\eta)(1+\zeta)(\xi-\eta+\zeta-2) \notag \\ &\dd{N_{15}}{\xi}&=&\frac{1}{8}(1-\eta)(1+\zeta)(2\xi-\eta+\zeta-1) \notag \\ &\dd{N_{15}}{\eta}&=&\frac{1}{8}(1+\xi)(1+\zeta)(-\xi+2\eta-\zeta+1) \notag \\ &\dd{N_{15}}{\zeta}&=&\frac{1}{8}(1+\xi)(1-\eta)(\xi-\eta+2\zeta-1) \notag \end{eqnarray} \begin{eqnarray} &N_{16}&=&\frac{1}{4}(1+\xi)(1-\eta \cdot \eta)(1+\zeta) \notag \\ &\dd{N_{16}}{\xi}&=&\frac{1}{4}(1-\eta \cdot \eta)(1+\zeta) \notag \\ &\dd{N_{16}}{\eta}&=&-\frac{1}{2}\eta(1+\xi)(1+\zeta) \notag \\ &\dd{N_{16}}{\zeta}&=&\frac{1}{4}(1+\xi)(1-\eta \cdot \eta) \notag \end{eqnarray} \begin{eqnarray} &N_{17}&=&\frac{1}{8}(1+\xi)(1+\eta)(1+\zeta)(\xi+\eta+\zeta-2) \notag \\ &\dd{N_{17}}{\xi}&=&\frac{1}{8}(1+\eta)(1+\zeta)(2\xi+\eta+\zeta-1) \notag \\ &\dd{N_{17}}{\eta}&=&\frac{1}{8}(1+\xi)(1+\zeta)(\xi+2\eta+\zeta-1) \notag \\ &\dd{N_{17}}{\zeta}&=&\frac{1}{8}(1+\xi)(1+\eta)(\xi+\eta+2\zeta-1) \notag \end{eqnarray} \begin{eqnarray} &N_{18}&=&\frac{1}{4}(1-\xi \cdot \xi)(1+\eta)(1+\zeta) \notag \\ &\dd{N_{18}}{\xi}&=&-\frac{1}{2}\xi(1+\eta)(1+\zeta) \notag \\ &\dd{N_{18}}{\eta}&=&\frac{1}{4}(1-\xi \cdot \xi)(1+\zeta) \notag \\ &\dd{N_{18}}{\zeta}&=&\frac{1}{4}(1-\xi \cdot \xi)(1+\eta) \notag \end{eqnarray} \begin{eqnarray} &N_{19}&=&\frac{1}{8}(1-\xi)(1+\eta)(1+\zeta)(-\xi+\eta+\zeta-2) \notag \\ &\dd{N_{19}}{\xi}&=&\frac{1}{8}(1+\eta)(1+\zeta)(2\xi-\eta-\zeta+1) \notag \\ &\dd{N_{19}}{\eta}&=&\frac{1}{8}(1-\xi)(1+\zeta)(-\xi+2\eta+\zeta-1) \notag \\ &\dd{N_{19}}{\zeta}&=&\frac{1}{8}(1-\xi)(1+\eta)(-\xi+\eta+2\zeta-1) \notag \end{eqnarray} \begin{eqnarray} &N_{20}&=&\frac{1}{4}(1-\xi)(1-\eta \cdot \eta)(1+\zeta) \notag \\ &\dd{N_{20}}{\xi}&=&-\frac{1}{4}(1-\eta \cdot \eta)(1+\zeta) \notag \\ &\dd{N_{20}}{\eta}&=&-\frac{1}{2}\eta(1-\xi)(1+\zeta) \notag \\ &\dd{N_{20}}{\zeta}&=&\frac{1}{4}(1-\xi)(1-\eta \cdot \eta) \notag \end{eqnarray}

形状関数の役立ち

この形状関数を用いると要素\(\,e\,\)内の任意点\(\,(\xi,\eta,\zeta)\,\)、すなわち直行座標系で \begin{equation} x=\sum_{i=1}^{20}N_ix_i \, , \quad y=\sum_{i=1}^{20}N_iy_i \, , \quad z=\sum_{i=1}^{20}N_iz_i \label{22} \end{equation} における変位\(\vec{u}\) は節点1～20の変位と形状関数を用いると、 \begin{equation} \vec{u}=\boldsymbol{N}\vec{u^{e}} \end{equation} と表わされます。ただし、 \begin{equation} \boldsymbol{N}= \begin{bmatrix} \boldsymbol{N}_1 & \boldsymbol{N}_2 & \cdots & \boldsymbol{N}_{20} \end{bmatrix} \quad ,\boldsymbol{N}_i= \begin{bmatrix} N_i & 0 & 0 \\ 0 & N_i & 0 \\ 0 & 0 & N_i \notag \end{bmatrix} \end{equation} \begin{equation} \vec{u^{e}}= \begin{bmatrix} u_1 & u_2 & \cdots & u_{20} \end{bmatrix}^{ \mathrm{T} } \notag \end{equation} です。歪みと応力についても同様ですが、まず、 \begin{equation} \boldsymbol{B}_i= \begin{bmatrix} \dd{N_i}{x} & 0 & 0 \\ 0 & \dd{N_i}{y} & 0 \\ 0 & 0 & \dd{N_i}{z} \\ \dd{N_i}{y} & \dd{N_i}{x} & 0 \\ 0 & \dd{N_i}{z} & \dd{N_i}{y} \\ \dd{N_i}{z} & 0 & \dd{N_i}{x} \end{bmatrix} \label{24} \end{equation} として\(\,\boldsymbol{B}\,\)マトリクスを定義すると、 \begin{equation} \vec{\varepsilon}= \begin{bmatrix} \dd{}{x} & 0 & 0 \\ 0 & \dd{}{y} & 0 \\ 0 & 0 & \dd{}{z} \\ \dd{}{y} & \dd{}{x} & 0 \\ 0 & \dd{}{z} & \dd{}{y} \\ \dd{}{z} & 0 & \dd{}{x} \end{bmatrix} \cdot \boldsymbol{N}\vec{u^{e}}= \begin{bmatrix} \dd{}{x} & 0 & 0 \\ 0 & \dd{}{y} & 0 \\ 0 & 0 & \dd{}{z} \\ \dd{}{y} & \dd{}{x} & 0 \\ 0 & \dd{}{z} & \dd{}{y} \\ \dd{}{z} & 0 & \dd{}{x} \end{bmatrix} \begin{bmatrix} \boldsymbol{N}_1 & \boldsymbol{N}_2 & \cdots & \boldsymbol{N}_{20} \end{bmatrix}\vec{u^{e}} \notag \end{equation} すなわち、 \begin{equation} \vec{\varepsilon}= \begin{bmatrix} \boldsymbol{B}_1 & \boldsymbol{B}_2 & \cdots & \boldsymbol{B}_{20} \end{bmatrix}\vec{u^{e}}=\boldsymbol{B}\vec{u^{e}} \label{25} \end{equation} と表すことができます。一方、応力は、 \begin{equation} \vec{\sigma} = \boldsymbol{D}\vec{\varepsilon}=\boldsymbol{D}\boldsymbol{B}\vec{u^{e}} \end{equation} と表わされます。このように形状関数を用いると、要素内の任意点における未知量を規定できるため、仮想仕事の原理より弾性方程式を離散化することができることとなります。